1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| clc,clear, close all
sj0=load('data12_1.txt');
x=sj0(:,1:2:8); x=x(:);
y=sj0(:,2:2:8); y=y(:);
sj=[x y]; d1=[70,40];
xy=[d1;sj;d1]; sj=xy*pi/180;
d=zeros(102);
for i=1:101
for j=i+1:102
d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*...
cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
end
end
d=d+d'; w=50; g=100;
for k=1:w
c=randperm(100);
c1=[1,c+1,102];
for t=1:102
flag=0;
for m=1:100
for n=m+2:101
if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<...
d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
c1(m+1:n)=c1(n:-1:m+1); flag=1;
end
end
end
if flag==0
J(k,c1)=1:102; break
end
end
end
J(:,1)=0; J=J/102;
for k=1:g
A=J;
c=randperm(w);
for i=1:2:w
F=2+floor(100*rand(1));
temp=A(c(i),[F:102]);
A(c(i),[F:102])=A(c(i+1),[F:102]);
A(c(i+1),F:102)=temp;
end
by=[];
while ~length(by)
by=find(rand(1,w)<0.1);
end
B=A(by,:);
for j=1:length(by)
bw=sort(2+floor(100*rand(1,3)));
B(j,:)=B(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]);
end
G=[J;A;B];
[SG,ind1]=sort(G,2);
num=size(G,1); long=zeros(1,num);
for j=1:num
for i=1:101
long(j)=long(j)+d(ind1(j,i),ind1(j,i+1));
end
end
[slong,ind2]=sort(long);
J=G(ind2(1:w),:);
end
path=ind1(ind2(1),:), flong=slong(1)
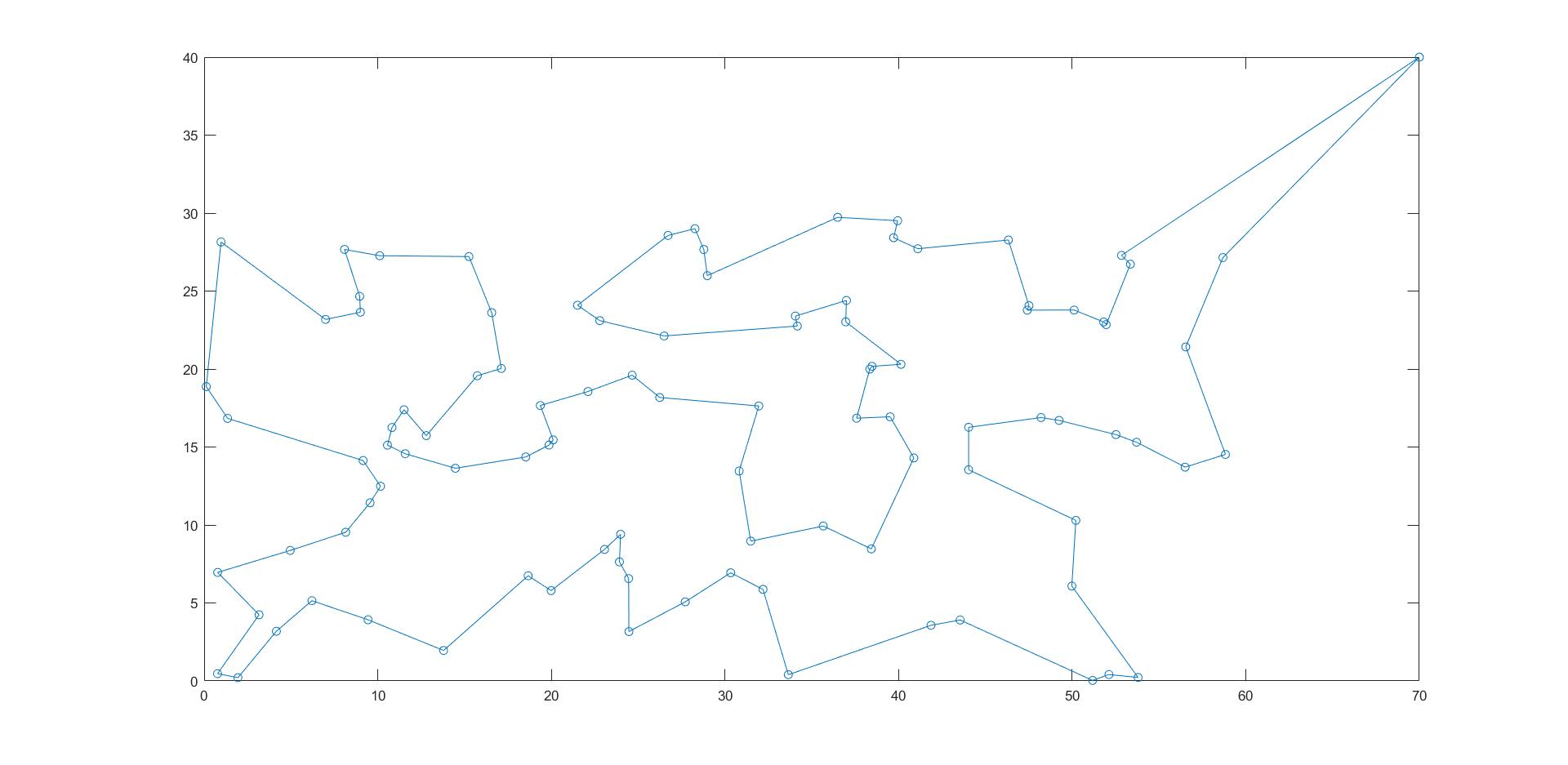
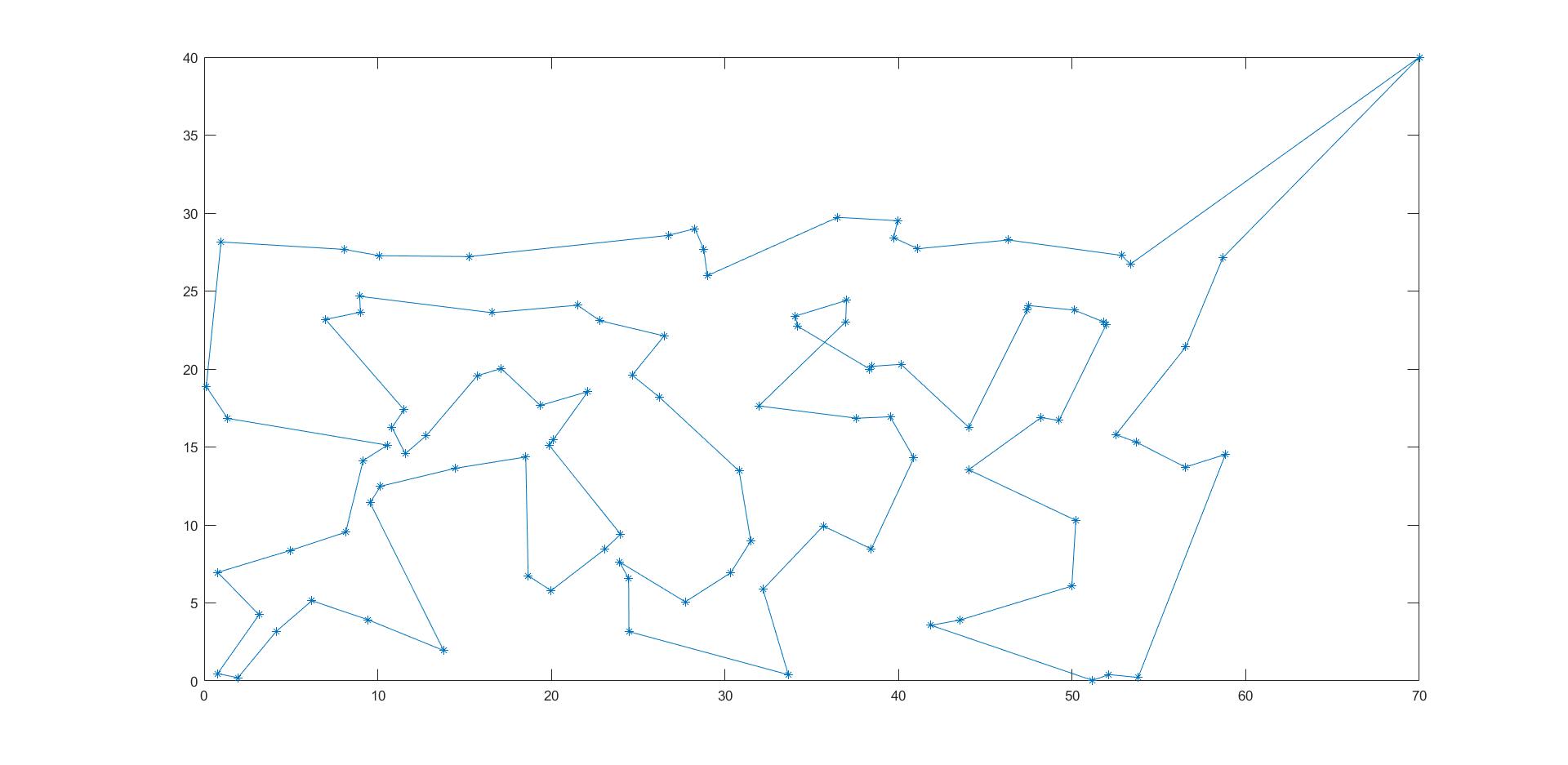
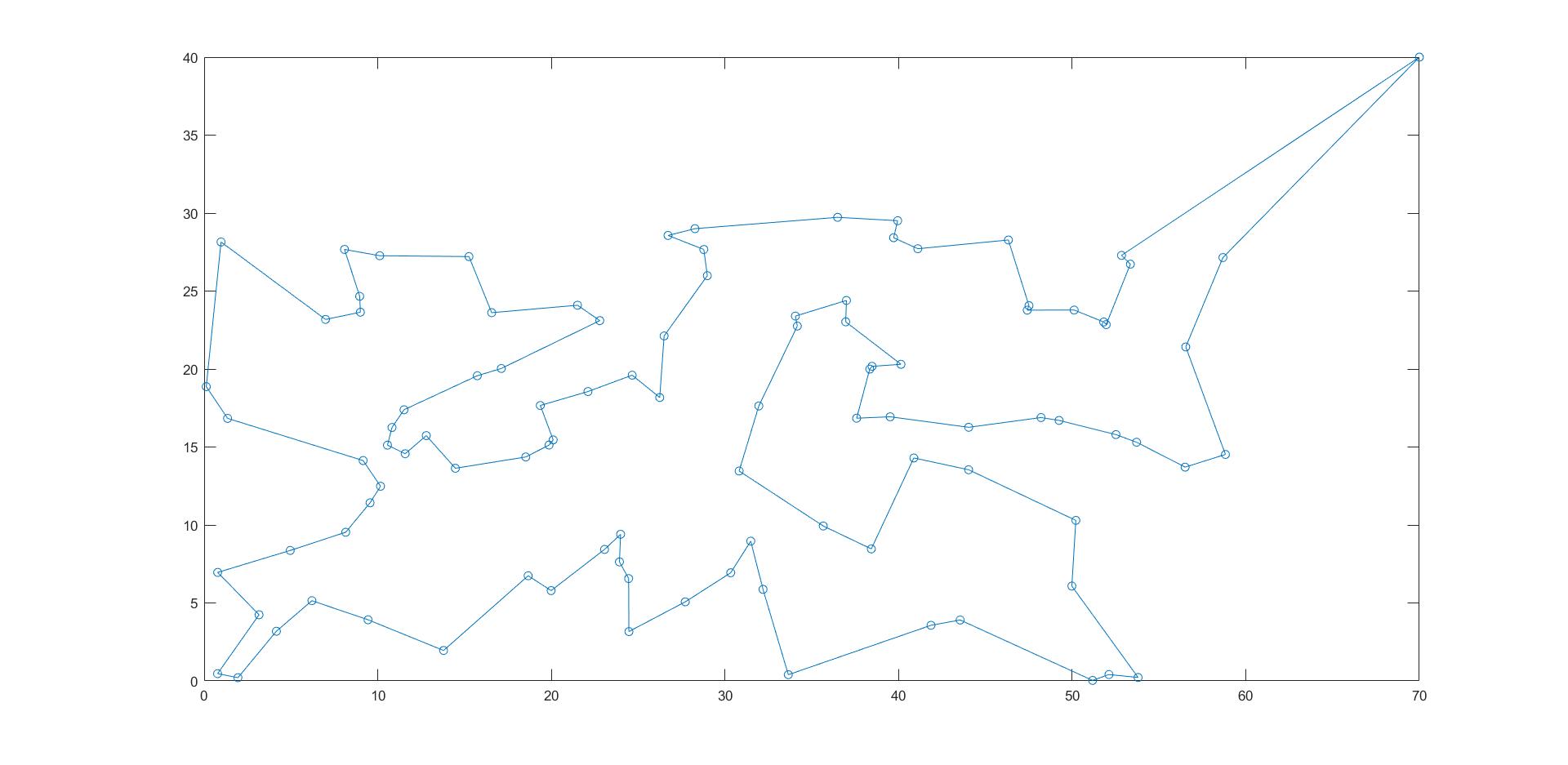
xx=xy(path,1);yy=xy(path,2);
plot(xx,yy,'-o')
|