有关MobleNet的笔记

李傲

发布于：2024年8月21日

次浏览

轻量级神经网络“巡礼”（二）—— MobileNet，从V1到V3 - 知乎 (zhihu.com)

标准卷积

标准卷积，利用若干个多通道卷积核对输入的多通道图像进行处理，输出的feature map既提取了通道特征，又提取了空间特征。

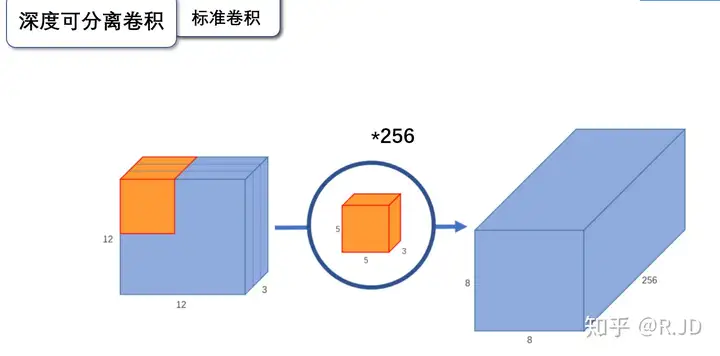
输入一个12×12×3的一个输入特征图，经过5×5×3的卷积核卷积得到一个8×8×1的输出特征图。如果此时我们有256个特征图，我们将会得到一个8×8×256的输出特征图。

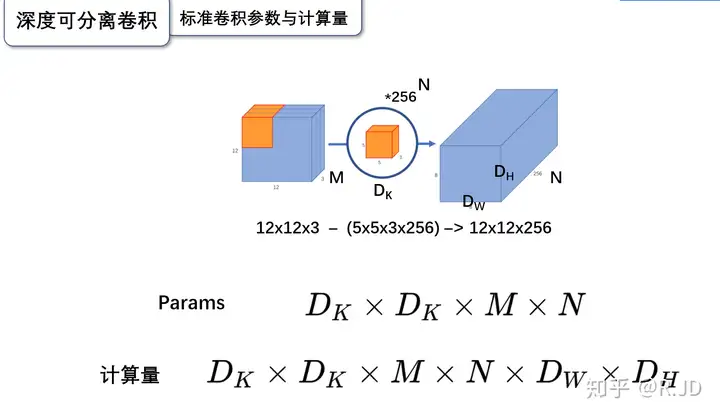
用数学公式表达标准卷积，假设卷积核大小为\(D_K*D_K\)，输入通道为M，输出通道为N，输出的特征图尺寸为\(D_W * D_H\)，则通过标准卷积之后，可以计算：

参数量为：\(D_K*D_K*M*N\) 计算量为：\(D_K*D_K*M*N*D_W * D_H\)

逐深度卷积（Depthwise Convolution）

简单理解，逐深度卷积就是深度(channel)维度不变，改变H/W。

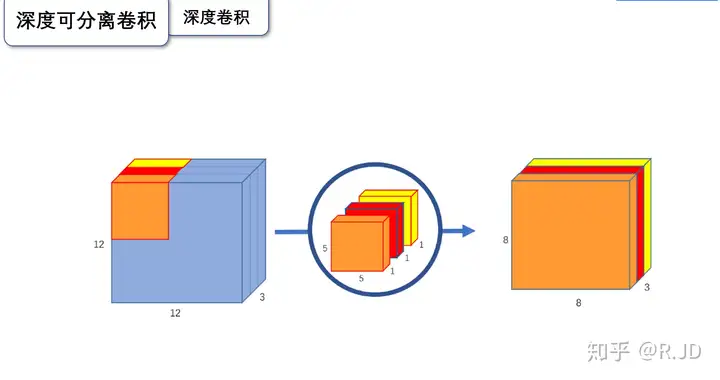
逐深度卷积（Depthwise convolution，DWConv）与标准卷积的区别在于，深度卷积的卷积核为单通道模式，需要对输入的每一个通道进行卷积，这样就会得到和输入特征图通道数一致的输出特征图。即有输入特征图通道数=卷积核个数=输出特征图个数。

逐点卷积（Pointwise Convolution）

简单理解，逐点卷积就是H/W维度不变，改变channel。

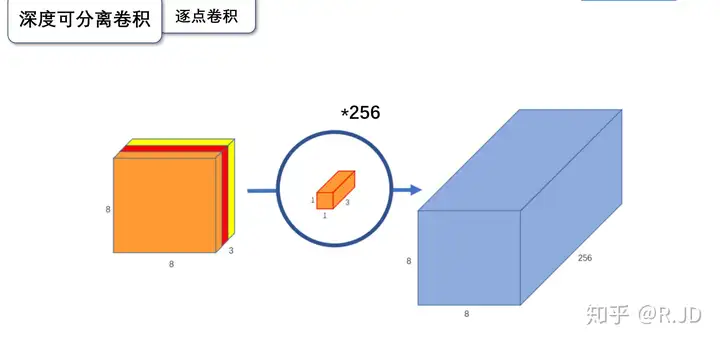
根据深度卷积可知，输入特征图通道数=卷积核个数=输出特征图个数，这样会导致输出的特征图个数过少（或者说输出特征图的通道数过少，可看成是输出特征图个数为1，通道数为3），从而可能影响信息的有效性。此时，就需要进行逐点卷积。

逐点卷积（Pointwise Convolution，PWConv）实质上是用1x1的卷积核进行升维。

深度可分离卷积（Depthwise Separable Convolution）

深度可分离卷积（Depthwise separable convolution, DSC）由逐深度卷积和逐点卷积组成，深度卷积用于提取空间特征，逐点卷积用于提取通道特征。深度可分离卷积在特征维度上分组卷积，对每个channel进行独立的逐深度卷积（depthwise convolution），并在输出前使用一个1x1卷积（pointwise convolution）将所有通道进行聚合。

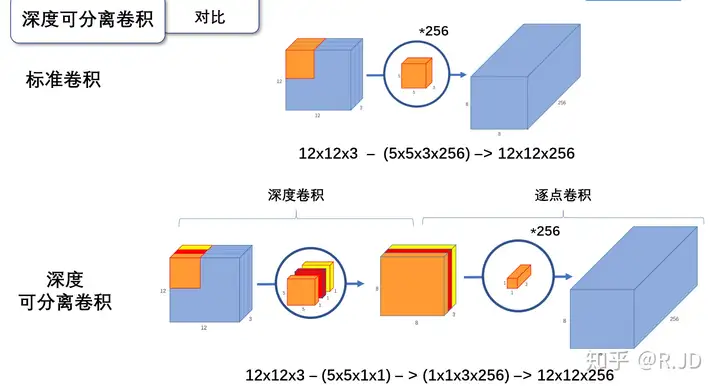
深度可分离卷积，先对每个channel进行DWConv，然后再通过 PWConv合并所有channels为输出特征图，从而达到减小计算量、提升计算效率的目的。

参数量

逐深度卷积：深度卷积的卷积核尺寸\(D_K * D_K * 1\)，卷积核个数为M，所以参数量为：\(D_K * D_K * M\)

逐点卷积：逐点卷积的卷积核尺寸为\(1*1*M\)，卷积核个数为N，所以参数量为：\(M *N\)

因此，深度可分离卷积的参数量为：\(D_K * D_K * M+M * N\)

计算量

逐深度卷积：深度卷积的卷积核尺寸\(D_K * D_K * 1\)，卷积核个数为M，每个都要做\(D_W * D_H\)次乘加运算，所以计算量为：\(D_K * D_K * M *D_W * D_H\)

逐点卷积：逐点卷积的卷积核尺寸为\(1 * 1 * M\)，卷积核个数为N，每个都要做\(D_W * D_H\)次乘加运算，所以计算量为：\(M*N * D_W * D_H\)

因此，深度可分离卷积的计算量为：\(D_K * D_K * M*D_W * D_H + M*N*D_W * D_H\)

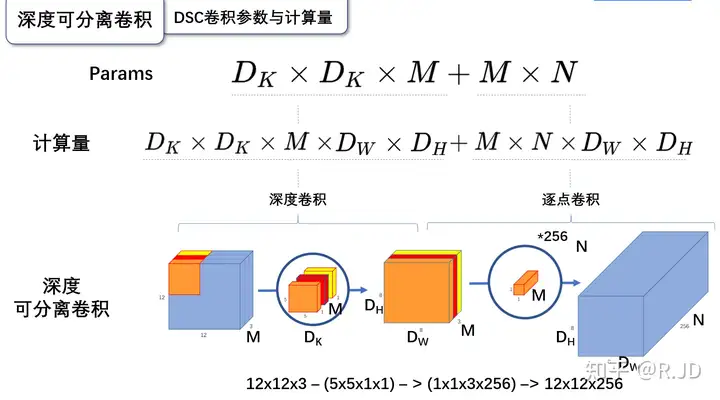
与标准卷积对比

结构对比

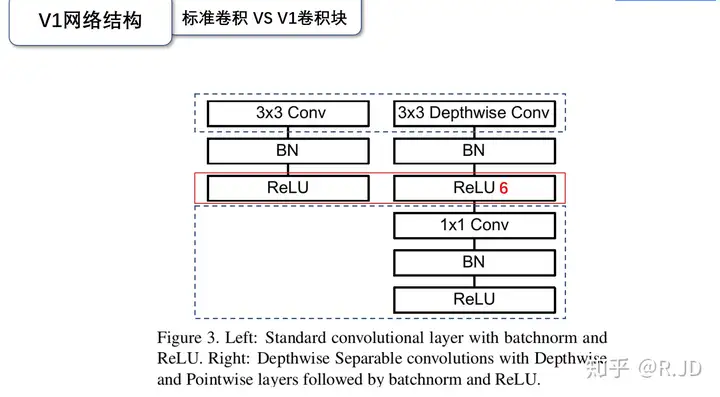
深度可分离卷积的每个块构成：首先是一个3x3的深度卷积，其次是BN、Relu层，接下来是1x1的逐点卷积，最后又是BN和Relu层。

计算量和参数量对比

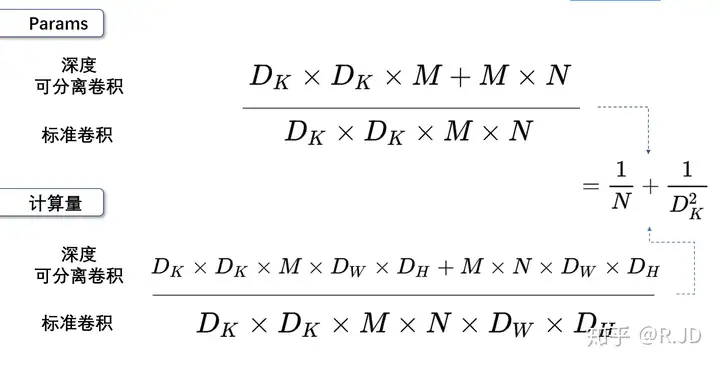
参数量比值=计算量比值=\(\frac{1}{N}+\frac{1}{D_k^2}\)

一般的，N较大，\(\frac{1}{N}\)可忽略不计，\(D_K\)表示卷积核的大小，若\(D_K =3\)，\(\frac{1}{D_k^2}=\frac{1}{9}\) 。也就是说，如果我们使用常见的3×3的卷积核，那么使用深度可分离卷积的参数量和计算量下降到原来的九分之一左右。

深度可分离卷积的优势

相比于传统的卷积神经网络，深度可分离卷积的显著优势在于：

更少的参数：可减少输入通道数量，从而有效地减少卷积层所需的参数。
更快的速度：运行速度比传统卷积快。
更加易于移植：计算量更小，更易于实现和部署在不同的平台上。
更加精简：能够精简计算模型，从而在较小的设备上实现高精度的运算。

(PyTorch)代码实现

torch.nn.Conv2d(in_channels, 
                out_channels, 
                kernel_size, 
                stride=1, 
                padding=0, 
                dilation=1, 
                groups=1, 
                bias=True, 
                padding_mode='zeros', 
                device=None, 
                dtype=None)

参数 groups 用来表示卷积的分组，in_channels 和 out_channels 都要被 groups 整除。当groups 设置不同时，可以区分出分组卷积或深度可分离卷积：

当 groups=1 时，表示标准卷积；
当 groups<in_channels 时，表示普通的分组卷积。例如，当 group=2 时，该分组卷积有两组并列的卷积，每组看到一半的输入通道，并产生一半的输出通道，最后将两组的结果连接起来。
当 groups=in_channels 时，表示深度可分离卷积，每个通道都有一组自己的滤波器。

MobileNet V2

对低维度做ReLU运算，很容易造成信息的丢失。而在高维度进行ReLU运算的话，信息的丢失则会很少。

这就解释了为什么深度卷积的卷积核有不少是空。发现了问题，我们就能更好地解决问题。针对这个问题，可以这样解决：既然是ReLU导致的信息损耗，将ReLU替换成线性激活函数。

Linear bottleneck

当然不能把所有的激活层都换成线性的，所以就把最后的那个ReLU6换成Linear。

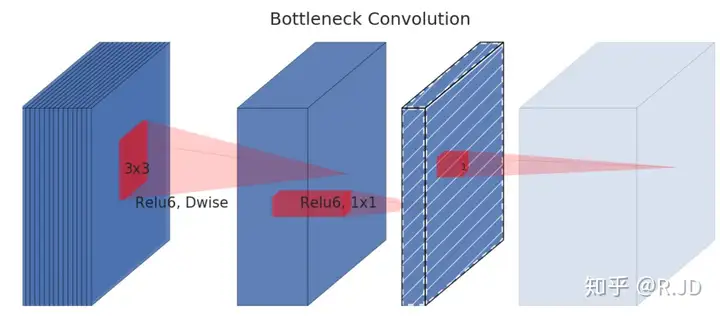
Separable with linear bottleneck

作者将这个部分称之为linear bottleneck。

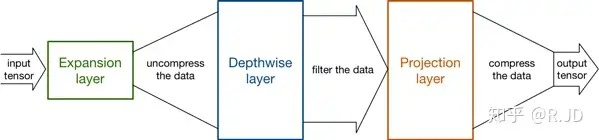
Expansion layer

现在还有个问题是，深度卷积本身没有改变通道的能力，来的是多少通道输出就是多少通道。如果来的通道很少的话，DW深度卷积只能在低维度上工作，这样效果并不会很好，所以我们要“扩张”通道。既然我们已经知道PW逐点卷积也就是1×1卷积可以用来升维和降维，那就可以在DW深度卷积之前使用PW卷积进行升维（升维倍数为t，t=6），再在一个更高维的空间中进行卷积操作来提取特征：

也就是说，不管输入通道数是多少，经过第一个PW逐点卷积升维之后，深度卷积都是在相对的更高6倍维度上进行工作。

Inverted residuals

回顾V1的网络结构，我们发现V1很像是一个直筒型的VGG网络。我们想像Resnet一样复用我们的特征，所以我们引入了shortcut结构，这样V2的block就是如下图形式：

对比一下ResNet和MobileNet V2：

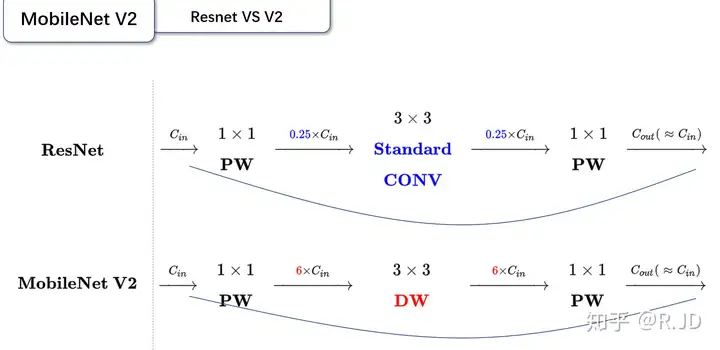
可以发现，都采用了 1×1 -> 3 ×3 -> 1 × 1 的模式，以及都使用Shortcut结构。但是不同点呢：

ResNet 先降维 (0.25倍)、卷积、再升维。
MobileNetV2 则是先升维 (6倍)、卷积、再降维。

刚好V2的block刚好与Resnet的block相反，作者将其命名为Inverted residuals。就是论文名中的Inverted residuals。

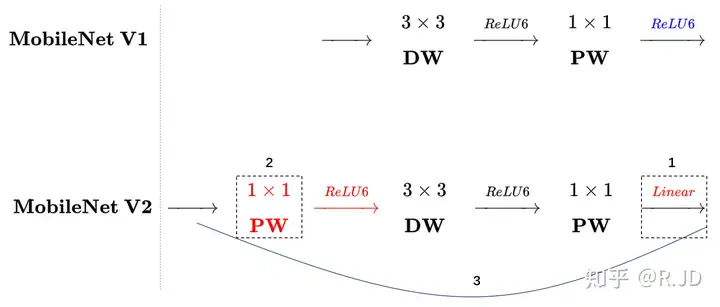
我们将V1和V2的block进行一下对比：

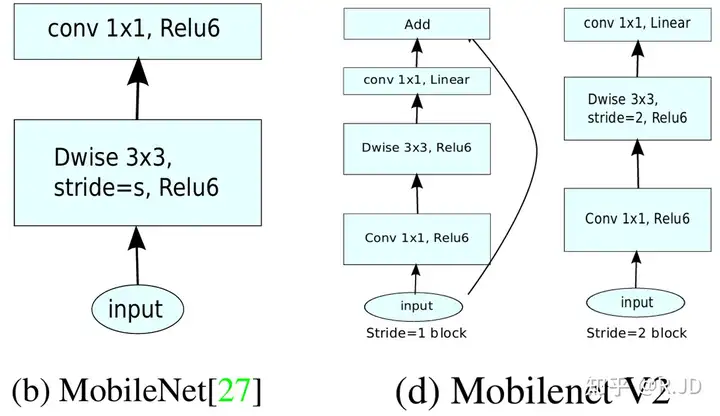
左边是v1的block，没有Shortcut并且带最后的ReLU6。

右边是v2的加入了1×1升维，引入Shortcut并且去掉了最后的ReLU，改为Linear。步长为1时，先进行1×1卷积升维，再进行深度卷积提取特征，再通过Linear的逐点卷积降维。将input与output相加，形成残差结构。步长为2时，因为input与output的尺寸不符，因此不添加shortcut结构，其余均一致。