有关流形（Manifold）和嵌入（Embedding）的笔记
流形，也就是 Manifold 。嵌入，也就是Embedding。
有时候经常会在paper里看到“嵌入在高维空间中的低维流形”，以及机器学习里的Embedding层。不过高维的数据对于我们这些可怜的低维生物来说总是很难以想像（论为什么要学习高等代数），所以最直观的例子通常都会是嵌入在三维空间中的二维或者一维流形。比如说一块布，可以把它看成一个二维平面，这是一个二维的欧氏空间，现在我们（在三维）中把它扭一扭，它就变成了一个流形（当然，不扭的时候，它也是一个流形，欧氏空间是流形的一种特殊情况）。
所以，直观上来讲，一个流形好比是一个\(d\)维的空间，在一个\(m\)维的空间中 (\(m\) > \(d\)) 被扭曲之后的结果。需要注意的是，流形并不是一个“形状”，而是一个“空间”。
再从球面说起，如果我们事先不知道球面的存在，那么球面上的点，其实就是三维欧氏空间上的点，可以用一个三元组来表示其坐标。但是和空间中的普通点不一样的是，它们允许出现的位置受到了一定的限制，具体到球面，可以可以看一下它的参数方程： \[ \begin{aligned} &x=x_{0}+r \sin \theta \cos \varphi \\ &y=y_{0}+r \sin \theta \sin \varphi \quad(0 \leq \varphi \leq 2 \pi \text { and } 0 \leq \theta \leq \pi) \\ &z=z_{0}+r \cos \theta \end{aligned} \] 可以看到，这些三维的坐标实际上是由两个变量 \(\theta\) 和 \(\varphi\) 生成的，也可以说成是它的自由度是2，也正好对应了它是一个二维的流形，这里有点让我想到了矩阵的秩，好像也是这个道理。
这个概念在深度学习领域最原初的切入点是所谓的Manifold Hypothesis（流形假设）。流形假设是指“自然的原始数据是低维的流形（Manifold）嵌入于（embedded in）原始数据所在的高维空间”。那么，深度学习的任务就是把高维原始数据（图像，句子）映射到低维流形，使得高维的原始数据被映射到低维流形之后变得可分，而这个映射就叫嵌入（Embedding）。
把流形引入到机器学习领域来主要有两种用途：一是将原来在欧氏空间中适用的算法加以改造，使得它工作在流形上，直接或间接地对流形的结构和性质加以利用；二是直接分析流形的结构，并试图将其映射到一个欧氏空间中，再在得到的结果上运用以前适用于欧氏空间的算法来进行学习。
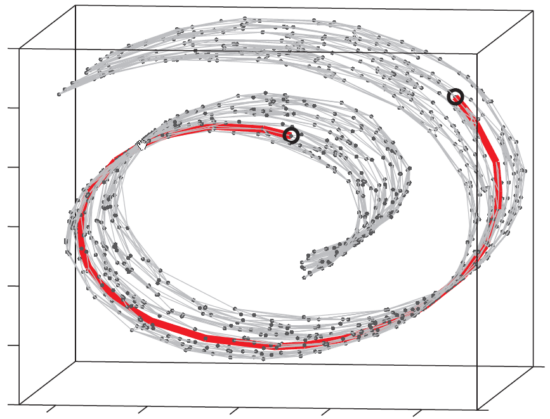
这个东西叫做 Swiss Roll ，姑且把它看作一块卷起来的布好了。图中两个标黑圈的点，如果通过外围欧氏空间中的欧氏距离来计算的话，会是挨得很近的点，可是在流形上它们实际上是距离很远的点：红色的线是 Isomap 求出来的流形上的距离。可以想像，如果是原始的 MDS 的话，降维之后肯定会是很暴力地直接把它投影到二维空间中，完全无视流形结构，而 Isomap 则可以成功地将流形“展开”之后再做投影。
最后码一个文章：https://blog.pluskid.org/archives/533
