这学期一直都在看ViT(Vision Transformer),现在的transformer近似于一种“大道至简”,在各个领域都可以作为一个baseline。
如果谈到Transformer那首先就会谈到self-attention。
Transformer是一个Sequence to Sequence model,特别之处在于它大量用到了self-attention。
要处理一个Sequence,最常想到的就是使用RNN,它的输入是一串vector sequence,输出是另一串vector sequence,如下图左所示是一个双向的RNN,同时考虑上下文。RNN非常擅长于处理input是一个sequence的状况,但它很不容易并行化 (hard to parallel)。
假设在单向RNN的情况下,要算出\(b_4\),就必须要先看\(a_1\)再看\(a_2\)再看\(a_3\)再看\(a_4\),所以这个过程很难平行处理。
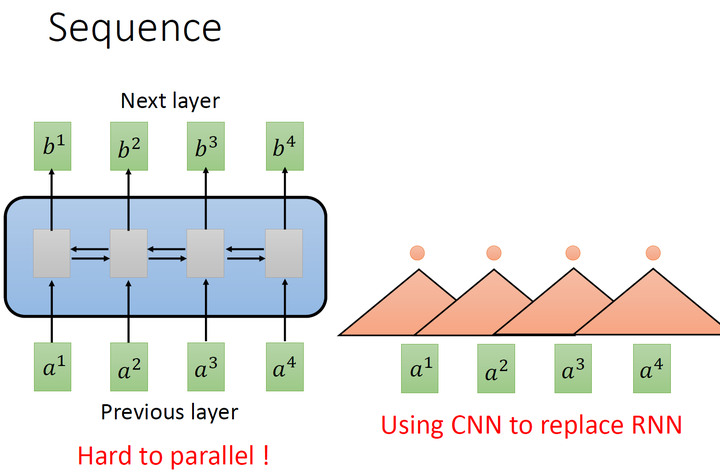
所以在并行化这个层面把CNN拿来取代RNN,如上图右所示。其中,橘色的三角形表示一个filter,每次扫过3个向量\(a\),扫过一轮以后,就输出了一排结果,使用橘色的小圆点表示。
这是第一个橘色的filter的过程,还有其他的filter,比如下图中的黄色的filter,它经历着与橘色的filter相似的过程,又输出一排结果,使用黄色的小圆点表示。
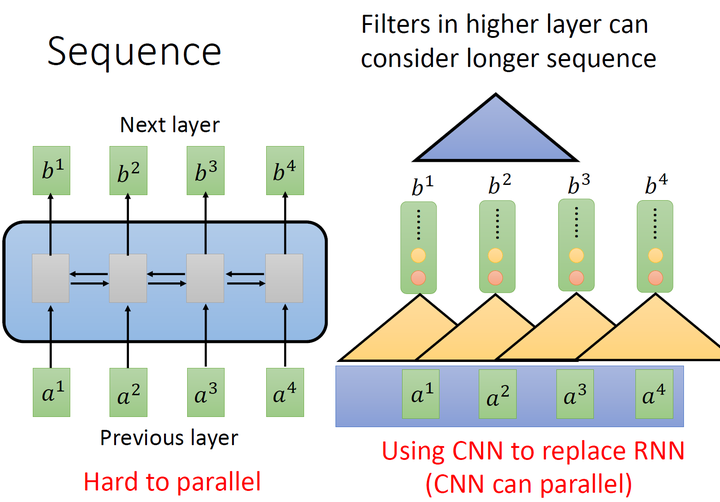
但是,表面上CNN和RNN可以做到相同的输入和输出,但是CNN只能考虑非常有限的内容。比如在我们右侧的图中CNN的filter只考虑了3个vector,不像RNN可以考虑之前的所有vector。但是CNN也不是没有办法考虑很长时间的dependency的,只需要堆叠filter,多堆叠几层,上层的filter就可以考虑比较多的资讯,比如,第二层的filter (蓝色的三角形)看了6个vector,所以,只要叠很多层,就能够看很长时间的资讯。
而CNN的一个好处是:它是可以并行化的 (can parallel),不需要等待红色的filter算完,再算黄色的filter。但是必须要叠很多层filter,才可以看到长时的资讯。
所以现在提出一个新的想法:self-attention,如下图所示,目的是使用self-attention layer取代RNN所做的事情。
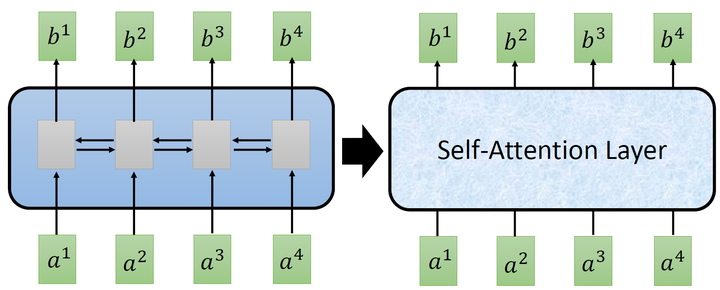
那么self-attention具体是怎么做的呢?
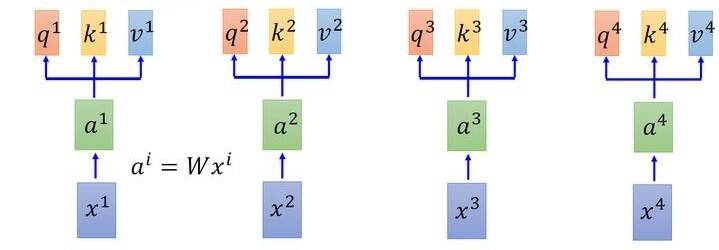
\(q:\)query (to match others) \[ q^{i}=W^{q} a^{i} \] \(k:\)key (to be matched) \[ k^{i}=W^{k} a^{i} \] \(v:\)value (information to be extracted) \[ v^{i}=W^{v} a^{i} \] 首先假设我们的input是下图的\(x_{1}-x_{4}\),是一个sequence,每一个input (vector)先乘上一个 矩阵\(W\)得到lembedding,即向量\(a_{1}-a_{4}\)。接着这个embedding进入 self-attention层,每 一个向量\(a_{1}-a_{4}\)分别乘上3个不同的transformation matrix\(W_{q}, W_{k}, W_{v}\),以向量\(a_{1}\)为 例,分别得到3个不同的向量\(q_{1}, k_{1}, v_{1}\)。
接下来使用每个query\(q\)去对每个key\(k\)做attention, attention就是匹配这2个向量有多接近, 比如我现在要对\(q^{i}\)和\(k^{j}\)做attention,我就可以把这2个向量做scaled inner product(按比例内积),得到\(\alpha_{i,j}\): \[ \alpha_{i,j}=q^{i} \cdot k^{j} / \sqrt{d} \] 式中,\(d\)是\(q\)跟\(k\)的维度。因为\(q \cdot k\)的数值会随着dimension的增大而增大,所以要除以\(\sqrt{\text { dimension }}\)的值,相当于归一化的效果。
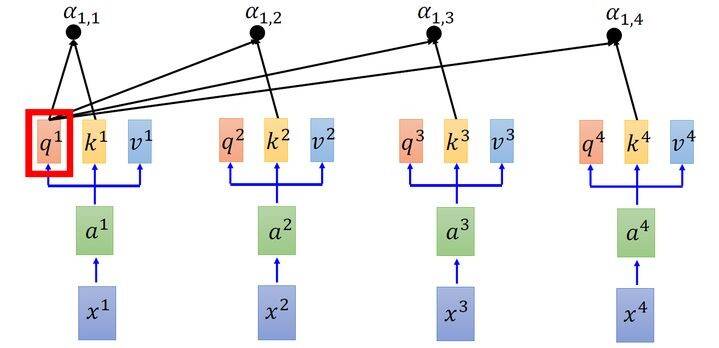
接下来要做的事如图6所示,把计算得到的所有\(\alpha_{1, i}\)值取 softmax 操作。
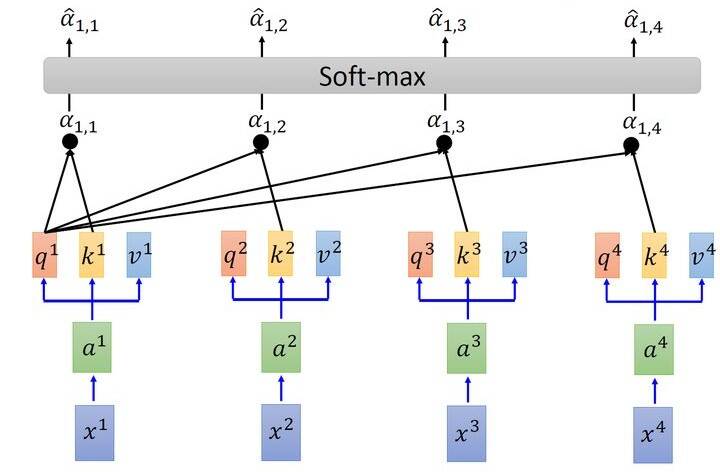
其中有: \[ \hat{\alpha}_{1, i}=\exp \left(\alpha_{1, i}\right) / \sum_{j} \exp \left(\alpha_{1, j}\right) \] 取完 softmax 操作以后,我们得到了\(\hat{\alpha}_{1, i}\),我们用它和所有的\(v^{i}\)值进行相乘。具体来讲, 把\(\hat{\alpha}_{1,1}\)乘上\(v^{1}\),把\(\hat{\alpha}_{1,2}\)乘上\(v^{2}\),把\(\hat{\alpha}_{1,3}\)乘上\(v^{3}\),把\(\hat{\alpha}_{1,4}\)乘上\(v^{4}\),把结果通通 加起来得到\(b^{1}\),所以,今天在产生\(b^{1}\)的过程中用了整个sequence的资讯 (Considering the whole sequence)。如果要考虑local的information,则只需要学习出相应的\(\hat{\alpha}_{1, i}=0\),\(b^{1}\)就不再带有那个对应分支的信息了;如果要考虑global的information,则只需要学习出相应的\(\hat{\alpha}_{1, i} \neq 0\),\(b^{1}\)就带有全部的对应分支的信息了。
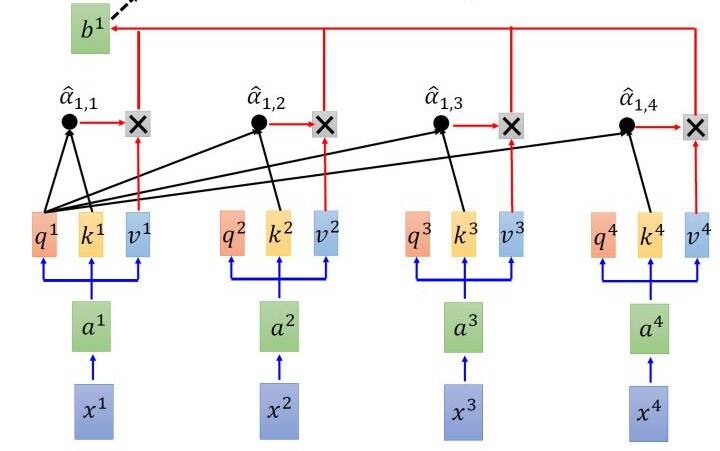
同样的方法,也可以计算出\(b^{2}, b^{3}, b^{4}\)。
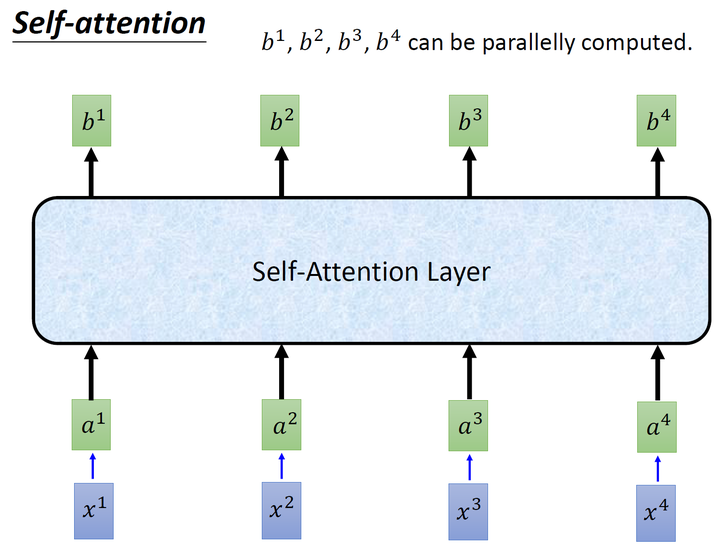
经过了以上一连串计算,self-attention layer做的事情跟RNN是一样的,只是它可以并行的得到layer输出的结果,如下图所示。现在我们要用矩阵表示上述的计算过程。
本例中我们选择三个输入值,已经通过embedding处理,得到了三个词向量。
1 | Input 1: [1, 0, 1, 0] |
权重包括三个,分别是query的\(W_{q} ,\)key的\(W_{k}\)以及value的\(W_{v}\),这三个权重分别初始化为
\(W_{q}\):
1 | [[1, 0, 1], |
\(W_{k}\):
1 | [[0, 0, 1], |
\(W_{v}\):
1 | [[0, 2, 0], |
有了输入和权重,接下来可以计算每个输入对应的key,query 和value了。
第一个输入的Key为:
1 | [0, 0, 1] |
第二个输入的Key为:
1 | [0, 0, 1] |
第三个输入的Key为:
1 | [0, 0, 1] |
同理我们计算value的结果为:
1 | [] |
最后我们计算query的结果:
1 | [] |
注意力的得分是通过query与每个key结果相乘。例如对于第一个query分别与三个key相乘,得到结果就是注意力得分。
计算结果为:
1 | [] |
softmax函数直接对上一步中的注意力得分做归一化处理。
1 | softmax([2, 4, 4]) = [0.0, 0.5, 0.5] |
上一步骤中输出结果求和就得到第一个输出值
1 | [0.0, 0.0, 0.0] |
重复计算,分别得到第二个和第三个输出值
于是三个输入经过self-attention模块,得到了三个输出值。这就是attention模块做的事情《Attention Is All You Need》论文中的attention计算公式: \[ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d}_{k}}\right) V \] attention最厉害的地方在于能够捕捉到全局信息,经过这个模块的输出结果,是通过输入结果两两运算得出了权重,再对输入进行加权求和得到了。除了捕捉全局信息,还能并行计算,这就比之前的RNN和CNN厉害多。



