triplet loss 是深度学习的一种损失函数,主要是用于训练差异性小的样本,比如人脸等;其次在训练目标是得到样本的embedding任务中,triplet loss 也经常使用,比如文本、图片的embedding。
损失函数公式:\(L=max(d(a,p)−d(a,n)+margin,0)\)
输入是一个三元组,包括锚(Anchor)示例、正(Positive)示例、负(Negative)示例,通过优化锚示例与正示例的距离小于锚示例与负示例的距离,实现样本之间的相似性计算。
a:anchor,锚示例;p:positive,与a是同一类别的样本;n:negative,与a是不同类别的样本;margin是一个大于0的常数。最终的优化目标是拉近a和p的距离,拉远a和n的距离。
其中样本可以分为三类:
easy triplets:\(L=0\),即\(d(a,p)+margin>d(a,n)\),这种情况不需要优化,天然a和p的距离很近,a和n的距离很远,如下图
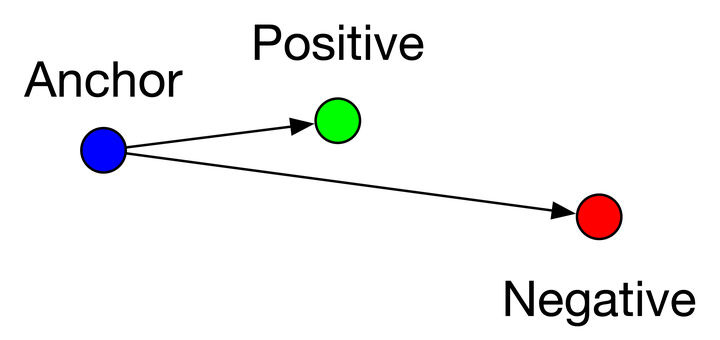
hard triplets:\(L>margin\),即\(d(a,p)>d(a,n)\),a和n的距离近,a和p的距离远,这种情况损失最大,需要优化,如下图
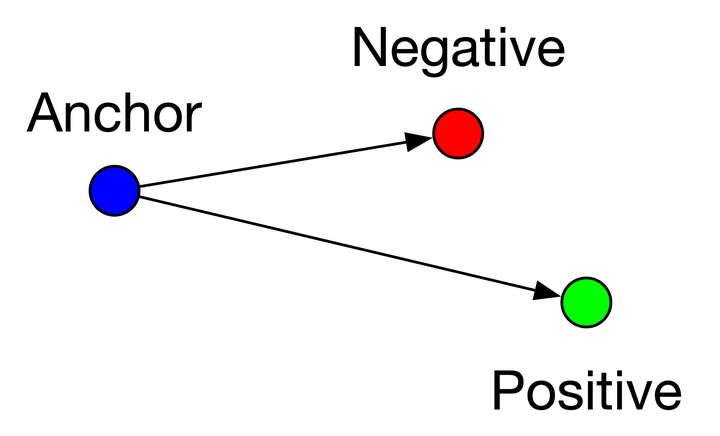
semi-hard triplets:\(L<margin\),即\(d(a,p)<d(a,n)<d(a,p)+margin\),即a和p的距离比a和n的距离近,但是近的不够多,不满足margin,这种情况存在损失,但损失比hard triplets要小,也需要优化,如下图
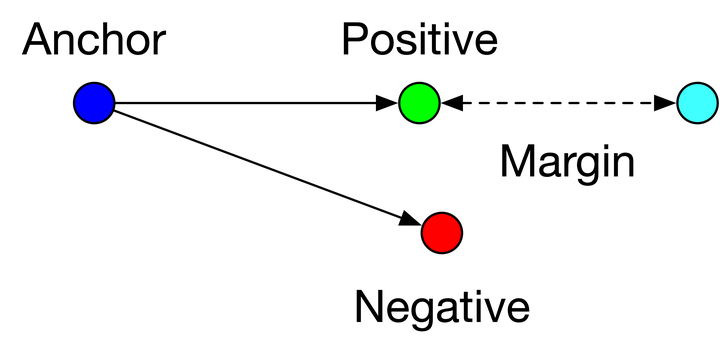
- 避免模型走捷径,将negative和positive的embedding训练成很相近,因为如果没margin,triplets loss公式就变成了 L=max(d(a,p)−d(a,n),0) ,那么只要 d(a,p)=d(a,n) 就可以满足上式,也就是锚点a和正例p与锚点a和负例n的距离一样即可,这样模型很难正确区分正例和负例。
- 设定一个margin常量,可以迫使模型努力学习,能让锚点a和负例n的distance值更大,同时让锚点a和正例p的distance值更小。
- 由于margin的存在,使得triplets loss多了一个参数,margin的大小需要调参。如果margin太大,则模型的损失会很大,而且学习到最后,loss也很难趋近于0,甚至导致网络不收敛,但是可以较有把握的区分较为相似的样本,即a和p更好区分;如果margin太小,loss很容易趋近于0,模型很好训练,但是较难区分a和p。
首先能看到,对于triplet loss的损失公式,要有3个输入,即锚点a,正例p和负例n。对于样本来讲,有3种,即easy triplets、hard triplets和semi-hard triplets。
理论上讲,使用hard triplets训练模型最好,因为这样模型能够有很好的学习能力,但由于margin的存在,这类样本可能模型没法很好的拟合,训练比较困难;其次是使用semi-hard triplet,这类样本是实际使用中最优选择,因为这类样本损失不为0,而且损失不大,模型既可以学习到样本之间的差异,又较容易收敛;至于easy triplet,损失为0,不用拿来训练。
针对不同的业务,其实构造的原则也不一样,比如人脸识别场景,样本的选择应该满足\(d(a,p)\)和\(d(a,n)\)尽可能接近,其实就是选择semi-hard triplets样本,这样一来,损失函数的公式不容易满足,也就意味着损失值不够低,模型必须认真训练和更新自己的参数,从而努力让\(d(a,n)\)的值尽可能变大,同时让\(d(a,p)\)的值尽可能变小。
针对搜索引擎场景,比如dssm,正样本是用户query搜索点击的doc做正例,负例是采用随机采样的策略,一般随机采样的策略是不可控的,既可能采样到easy triplet,又可能采样到hard triple,要看采样的池子怎么确定。
Facebook最近提出的EBR也指出,在随机采样的策略上,要增加semi-hard triplets,选取搜索曝光页面第101~500,也就是让模型看到这些模糊的样本,有些相似但没那么相似,这样模型才能更好的学习到样本之间的差异。



