还有一个问题是:现在的self-attention中没有位置的信息,一个单词向量的“近在咫尺”位置的单词向量和“远在天涯”位置的单词向量效果是一样的,没有表示位置的信息(No position information in self attention)。
所以输入”A打了B“或者”B打了A“的效果其实是一样的,因为并没有考虑位置的信息。所以在self-attention原来的paper中,作者为了解决这个问题所做的事情是如下图所示:
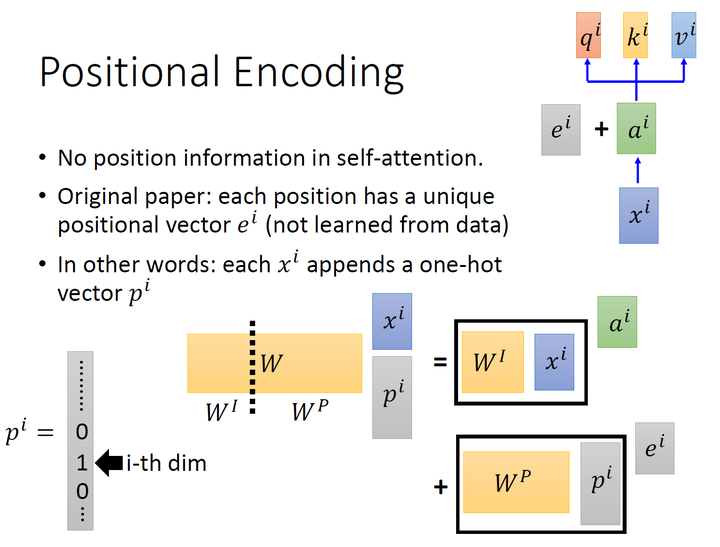
具体的做法是: 给每一个位置规定一个表示位置信息的向量\(e^{i}\),让它与\(a^{i}\)加在一起之后作为 新的\(a^{i}\)参与后面的运算过程,但是这个向量\(e^{i}\)是由人工设定的,而不是神经网络学习出来的,每一个位置都有一个不同的\(e^{i}\)。
但是这里可能就会出现一个问题:为什么是相加而不是concatenate?加起来以后,原来表示位置的资讯不就混到里面去,很难被找到了吗?
如上图所示,我们先给每一个位置的\(x^{i} \in R(d, 1)\)append一个one-hot编码的向量\(p^{i} \in R(N, 1)\),得到一个新的输入向量\(x_{p}^{i} \in R(d+N, 1)\),这个向量作为新的输入,乘 以一个transformation matrix\(W=\left[W^{I}, W^{P}\right] \in R(d, d+N)\)。那么: \[ W \cdot x_{p}^{i}=\left[W^{I}, W^{P}\right] \cdot\left[\begin{array}{c} x^{i} \\ p^{i} \end{array}\right]=W^{I} \cdot x^{i}+W^{P} \cdot p^{i}=a^{i}+e^{i} \] Transformer中除了单词的Embedding,还需要使用位置Embedding表示单词出现在句子中的位置。因为Transformer不采用双向RNN的结构,而是使用全局信息,不能利用单词的顺序信息,而这部分信息对于NLP来说非常重要。所以Transformer中使用位置Embedding保存单词在序列中的相对或绝对位置。
位置Embedding用PE表示,PE的维度与单词Embedding是一样的。PE可以通过训练得到,也可以使用某种公式计算得到。在 Transformer 中采用了后者,计算公式如下: \[ \begin{aligned} P E_{(p o s, 2 i)} &=\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(\text {pos }, 2 i+1)} &=\cos \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \end{aligned} \] 式中,pos表示token在sequence中的位置。
\(i\),或者准确意义上是\(2 i\)和\(2 i+1\)表示了Positional Encoding的维度,\(i\)的取值范围是:\(\left[0, \ldots, d_{\text {model }} / 2\right)\)。所以当 pos 为 1 时,对应的Positional Encoding可以写成: \[ P E(1)=\left[\sin \left(1 / 10000^{0 / 512}\right), \cos \left(1 / 10000^{0 / 512}\right), \sin \left(1 / 10000^{2 / 512}\right), \cos \left(1 / 10000^{2 / 512}\right), \ldots\right] \] 式中,\(d_{\text {model }}=512\)。底数是 10000 。
这个式子的好处是:
- 每个位置有一个唯一的positional encoding。
- 使PE能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有 20 个单词,突然来了一个长度为 21 的句子,则使用公式计算的方法可以计算出第 21 位的 Embedding。
- 可以让模型容易地计算出相对位置,对于固定长度的间距\(k\),任意位置的\(PE_{pos+k}\)都可以被\(PE_{pos}\)的线性函数表示。



