今天来填一个巨大的坑,主要是学车真的快把人热傻了外加晒成了黑炭,考不过真是be了。
神经网络叠的越深,则学习出的效果就一定会越好吗?答案无疑是否定的,人们发现当模型层数增加到某种程度,模型的效果将会不升反降。也就是说,深度模型发生了退化(degradation)情况。
那么,为什么会出现这种情况?
首先印入脑海的就是的过拟合问题
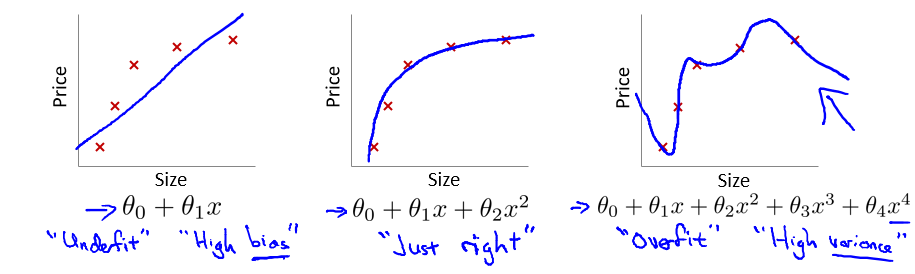
在这个多项式回归问题中,左边的模型是欠拟合(under fit)的此时有很高的偏差(high bias),中间的拟合比较成功,而右边则是典型的过拟合(overfit),此时由于模型过于复杂,导致了高方差(high variance)。
然而,很明显当前CNN面临的效果退化不是因为过拟合,因为过拟合的现象是"高方差,低偏差",即测试误差大而训练误差小。但实际上,深层CNN的训练误差和测试误差都很大。
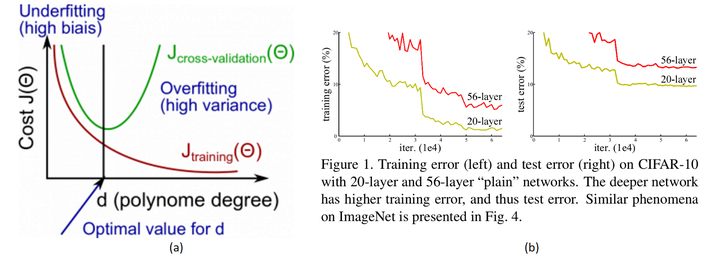
CIFAR-10上的训练误差(左)和测试误差(右),具有20层和56层“普通”网络。网络越深,训练误差越大,因此测试误差越大。
除此之外,最受人认可的原因就是“梯度爆炸/消失(弥散)”了。为了理解什么是梯度弥散,首先回顾一下反向传播的知识。
假设我们现在需要计算一个函数\(f(x, y, z)=(x+y) \times z, \quad x=-2, y=5, z=-4\)在时的梯度,那么首先可以做出如下所示的计算图。
将\(x=-2, y=5, z=-4\)带入,其中,令\(x+y=q\),一步步计算,很容易就能得出\(f(-2,5,-4)=-12\)。
这就是前向传播,即: \[ \left\{\begin{array}{l} f=q \cdot z \\ q=x+y \end{array}\right. \] 前向传播是从输入一步步向前计算输出,而反向传播则是从输出反向一点点推出输入的梯度。 \[ \left\{\begin{array}{l} \frac{d f}{d q}=z \\ \frac{d f}{d z}=q \\ \frac{d f}{d x}=\frac{d f}{d q} \cdot \frac{d q}{d x}, \frac{d f}{d y}=\frac{d f}{d q} \cdot \frac{d q}{d y} \end{array}\right. \]

观察上述反向传播,不难发现,在输出端梯度的模值,经过回传扩大了3~4倍。
这是由于反向传播结果的数值大小不止取决于求导的式子,很大程度上也取决于输入的模值。当计算图每次输入的模值都大于1,那么经过很多层回传,梯度将不可避免地呈几何倍数增长,每次都变成3~4倍,重复上万次,直到Nan。这就是梯度爆炸现象。
当然反过来,如果我们每个阶段输入的模恒小于1,那么梯度也将不可避免地呈几何倍数下降,这就是梯度消失现象。值得一提的是,由于人为的参数设置,梯度更倾向于消失而不是爆炸。
由于至今神经网络都以反向传播为参数更新的基础,所以梯度消失问题听起来很有道理。然而,事实也并非如此,至少不止如此。
我们现在无论用Pytorch还是Tensorflow,都会自然而然地加上Bacth Normalization(批标准化),而BN的作用本质上也是控制每层输入的模值,因此梯度的爆炸/消失现象理应在很早就被解决了,至少解决了大半。
不是过拟合,也不是梯度消失,CNN没有遇到我们熟知的两个老大难问题,却还是随着模型的加深而导致效果退化。无需任何数学论证,我们都会觉得这不符合常理。
按理说,当我们堆叠一个模型时,理所当然的会认为效果会越堆越好。因为,假设一个比较浅的网络已经可以达到不错的效果,那么即使之后堆上去的网络什么也不做,模型的效果也不会变差。
然而事实上,这却是问题所在。“什么都不做”恰好是当前神经网络最难做到的东西之一。
MobileNet V2的论文也提到过类似的现象,由于非线性激活函数Relu的存在,每次输入到输出的过程都几乎是不可逆的(信息损失)。我们很难从输出反推回完整的输入。

在这些示例中,使用随机矩阵\(T\)将初始螺旋嵌入到n维空间中,然后使用\(T^{-1}\)将其投影回二维空间。在上述示例中,n=2,3导致信息损失,其中流形的某些点彼此塌陷,而对于n=15到30,变换是高度非凸的。
也许赋予神经网络无限可能性的“非线性”也使得特征随着层层前向传播得到完整保留(什么也不做)的可能性都微乎其微。
用学术点的话说,这种神经网络丢失的“不忘初心”/“什么都不做”的品质叫做恒等映射(identity mapping)。
因此,可以认为Residual Learning的初衷,其实是让模型的内部结构至少有恒等映射的能力。以保证在堆叠网络的过程中,网络至少不会因为继续堆叠而产生退化!
前面分析得出,如果深层网络后面的层都是是恒等映射,那么模型就可以转化为一个浅层网络。那现在的问题就是如何得到恒等映射了。
事实上,已有的神经网络很难拟合潜在的恒等映射函数\(H(x) = x\)。
但如果把网络设计为\(H(x) = F(x) + x\),即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数\(F(x) = H(x) - x\).
只要\(F(x)=0\),就构成了一个恒等映射\(H(x) = x\)。 而且,拟合残差至少比拟合恒等映射容易得多。
于是,就有了论文中的Residual block结构
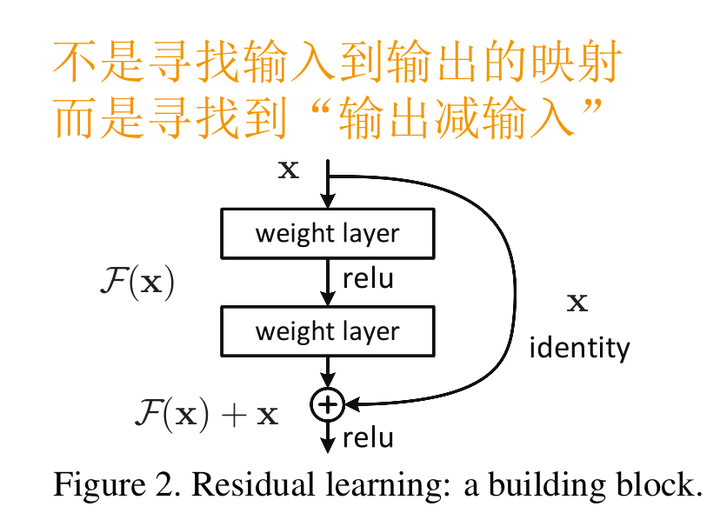
图中右侧的曲线叫做跳接(shortcut connection),通过跳接在激活函数前,将上一层(或几层)之前的输出与本层计算的输出相加,将求和的结果输入到激活函数中做为本层的输出。
用数学语言描述,假设Residual Block的输入为\(x\),则输出\(y\)等于: \[ \mathbf{y}=\mathcal{F}\left(x,\left\{W_{i}\right\}\right)+x \] 其中\(F(x,{Wi})\)是我们学习的目标,即输出输入的残差\(y−x\)。以上图为例,残差部分是中间有一个Relu激活的双层权重,即: \[ \mathcal{F}=W_{2} \sigma\left(W_{1} x\right) \] 其中\(σ\)指代Relu,而 W1,W2 指代两层权重。
顺带一提,这里一个Block中必须至少含有两个层,否则就会出现很滑稽的情况: \[ \mathbf{y}=\mathcal{F}\left(x,\left\{W_{i}\right\}\right)+x=\left(W_{1} x\right)+x=\left(W_{1}+1\right) x \] 显然这样加了和没加差不多
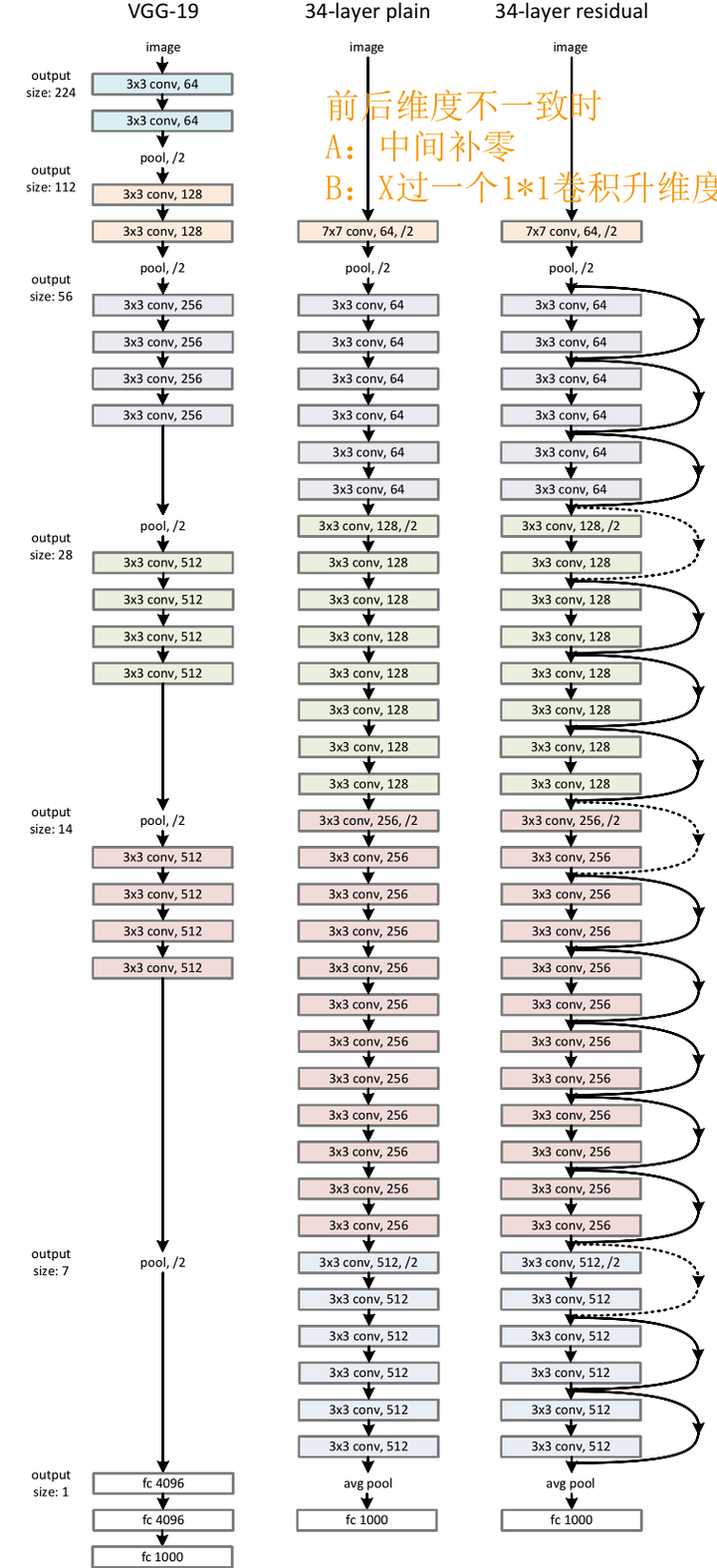
可以看到即使是当年号称“Very Deep”的VGG,和最基础的Resnet在深度上都相形见绌。
跳接的曲线中大部分是实线,但也有少部分虚线。这些虚线的代表这些Block前后的维度不一致,因为去掉残差结构的Plain网络还是参照了VGG经典的设计思路:每隔x层,空间上/2(下采样)但深度翻倍。
也就是说,维度不一致体现在两个层面:空间上不一致、深度上不一致
空间上不一致很简单,只需要在跳接的部分给输入x加上一个线性映射\(Ws\),即:
\[
\mathbf{y}=\mathcal{F}\left(\mathbf{x},\left\{W_{i}\right\}\right)+\mathbf{x}
\quad \rightarrow \quad
\mathbf{y}=\mathcal{F}\left(\mathbf{x},\left\{W_{i}\right\}\right)+W_{s}
\mathbf{x}
\]
而对于深度上的不一致,则有两种解决办法,一种是在跳接过程中加一个1*1的卷积层进行升维,另一种则是直接简单粗暴地补零。事实证明两种方法都行得通。
论文认为即使BN过后梯度的模稳定在了正常范围内,但梯度的相关性实际上是随着层数增加持续衰减的。而经过证明,ResNet可以有效减少这种相关性的衰减。
对于\(L\)层的网络来说,没有残差表示的Plain Net梯度相关性的衰减在\(\frac{1}{2^{L}}\) ,而ResNet的衰减却只有\(\frac{1}{\sqrt{L}}\)。这也验证了ResNet论文本身的观点,网络训练难度随着层数增长的速度不是线性,而至少是多项式等级的增长,也可能是指数级增长的。
而对于“梯度弥散”观点来说,在输出引入一个输入x的恒等映射,则梯度也会对应地引入一个常数1,这样的网络的确不容易出现梯度值异常,在某种意义上,起到了稳定梯度的作用。除此之外,shortcut类似的方法也并不是第一次提出,之前就有“Highway Networks”。可以只管理解为,以往参数要得到梯度,需要快递员将梯度一层一层中转到参数手中,而跳接实际上给梯度开了一条“高速公路”,效率自然大幅提高,不过这只是个比较想当然的理由。



